LeetCode28.找出字符串中第一个匹配项的下标

发表于 更新于 分类于 阅读次数： 本文字数： 2.9k 阅读时长 ≈ 3 分钟

LeetCode28.找出字符串中第一个匹配项的下标【easy】。本文参考 https://zhuanlan.zhihu.com/p/105629613。

题目描述

给你两个字符串 haystack 和 needle ，请你在 haystack 字符串中找出 needle 字符串的第一个匹配项的下标（下标从 0 开始）。如果 needle 不是 haystack 的一部分，则返回 -1 。

输入输出示例

示例 1：
输入：haystack = “sadbutsad”, needle = “sad”
输出：0
解释：”sad” 在下标 0 和 6 处匹配。
第一个匹配项的下标是 0 ，所以返回 0 。

示例 2：
输入：haystack = “leetcode”, needle = “leeto”
输出：-1
解释：”leeto” 没有在 “leetcode” 中出现，所以返回 -1 。

提示：

  • 1 <= haystack.length, needle.length <= 104
  • haystack 和 needle 仅由小写英文字符组成

题目分析

字符串匹配，暴力方法就是使用两次 for 循环来进行比较，将 needle[0] 与 haystack[0] 左边对齐比较，如果相同就比较 needle[1] 与 haystack[1]，否则就将 needle 右移一位，比较 needle[0] 与 haystack[1]，以此类推，直到找到结果。这种方法最坏的结果就是每次比到最后一个才发现不对，又要从第一位开始对比，最坏的时间复杂度就是 O(m*n)。
优化这个算法，可以考虑 KMP，这是字符串匹配的常用算法。我们将被匹配的主串称为 txt，用于匹配的模式串称为 pat，i 是指向 txt 的指针，j 是指向 pat 的指针，KMP 的核心思想在于，不回退 txt 的指针 i（不会重复扫描 txt），而是借助储存的信息把 pat 移到正确的位置继续匹配，是一种以空间换时间的方法。在每一次匹配过程中，我们就能够判断后续几次匹配是否会成功，从而减少比较的次数。
例如，比较 txt: abababcabaa 和 pat: ababcabaa，如果采用暴力的方法，当比较到 txt[4] 和 pat[4] 时，a 和 c 不匹配，我们又要从 txt [1] 和 pat[0] 开始比较。但如果不进行回溯，即从 txt[4] 和 pat[0] 开始比较，又可能会漏掉一部分匹配。为了让 j 设置为一个合适的值，我们引入了 PMT（部分匹配表）。j 值应该被赋值为多少，只与模式串自身有关，每个模式串都对应着一张 PMT，用 p 代表模式串数组，pmt[i] 的值是子字符串 p[0:i] 的前缀集合与后缀集合的交集中最长元素的长度（如果字符串 A 和 B ，存在 A=BS，其中 S 是任意的非空字符串，那就称 B 为 A 的前缀，例如字符串 “Hello”，其前缀集合就是 {“H”,”He”,”Hel”,”Hell”}）。
举例来说就是对于 ababcab，可以得到这样一张 pmt 表：
KMP
当我们匹配失败时，例如上述 txt[4] = a 和 pat[4] = c 不匹配，由 pmt 表我们可知，在 c 之前，有一个前缀 ab 和 txt 开头 ab 是匹配的（pmt[j - 1] = 2），所以我们可以直接用 txt[4] 和 pat[2] 比较，所以令 j = pmt[j - 1]，可以减少回退次数。当然，我们不一定能匹配成功，有可能 j 一路减到了0，但是 txt[i] 仍然不等于 pat[j]，这时，我们不再移动 j 指针，而是老老实实地从头开始比较。
由上可知，如果是在 j 位 失配，那么 j 指针回溯的位置的其实是第 j −1 位的 PMT 值。所以为了编程方便，我们往往会把 PMT 整体向右移一位，得到一个 next 数组，同时令 next[0]=-1，表示在每一位匹配失败时应跳转到的索引。也就是说，匹配失败时按照 i -> next[i] -> next[next[i]] -> …的顺序跳转。
那么问题就来了，PMT 怎么求？暴力求法时间复杂度是 O(n^2)，但我们可以通过一种精妙的方式来解决。我们可以在错开一位后，让 p 自己匹配自己，在这个过程中记录 j 值，更新 pmt。为什么可以这样做呢？我们可以思考一下。
https://www.zhihu.com/question/21923021/answer/281346746一文有一个很好的解释和示例：求 next 数组的过程，其实就可以看成一个字符串匹配的过程。我们以模式字符串为主串，以模式字符串的前缀为匹配串，一旦匹配成功，那么当前的 next 值就是匹配成功的子字符串的长度，即我们从模式字符串的第一位开始（不包括第0位），与自己进行匹配，在任一位置能匹配的最长长度就是当前位置的 next 值。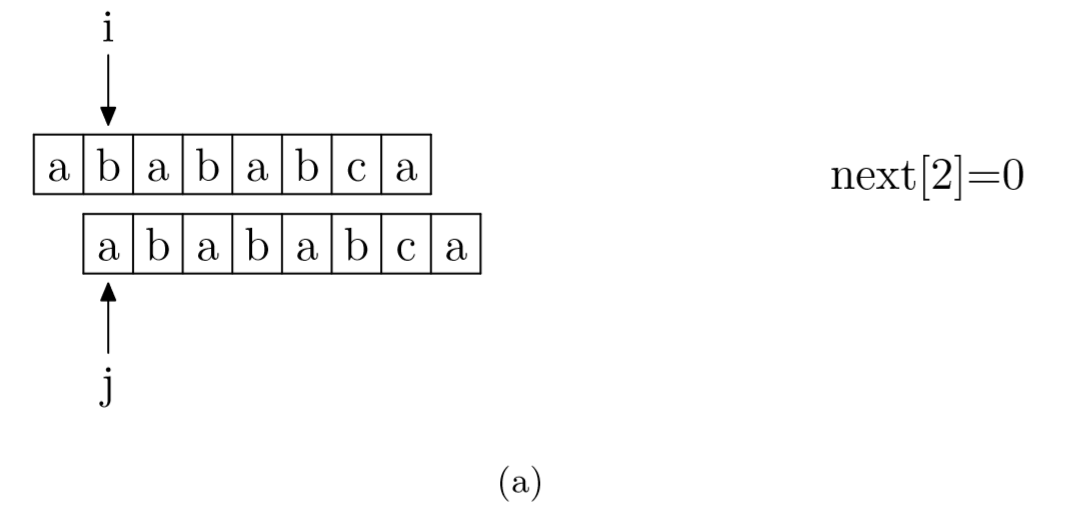
next_a
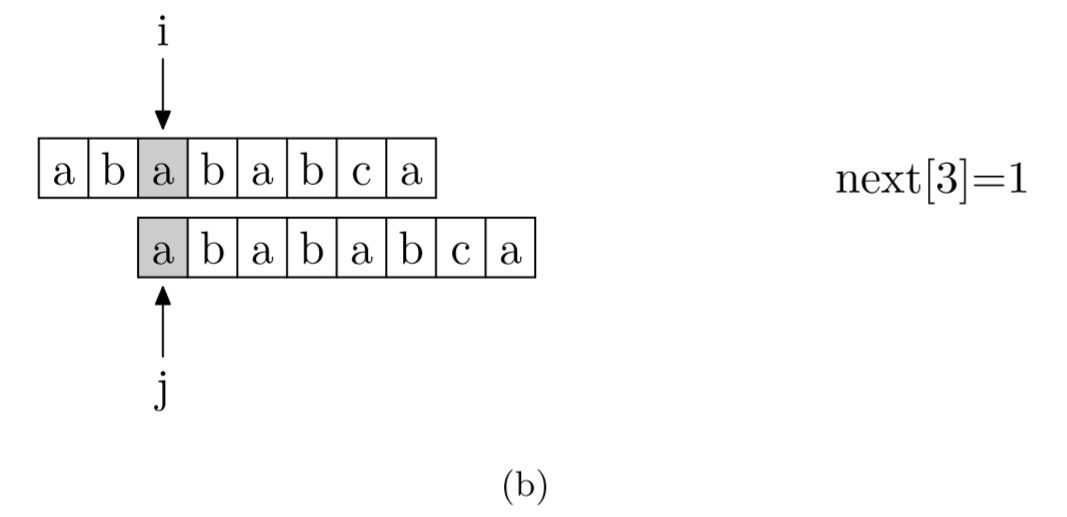
next_b
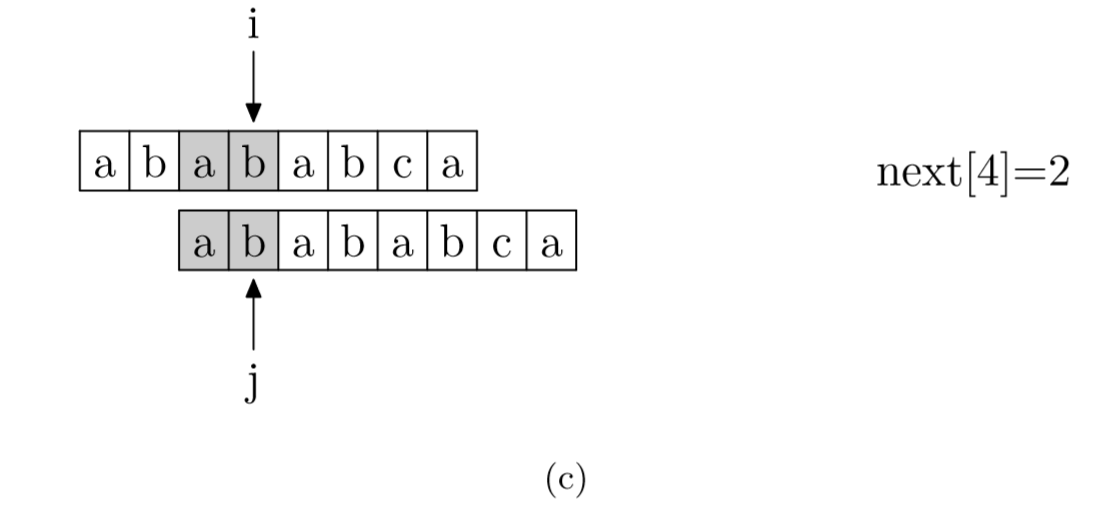
next_c
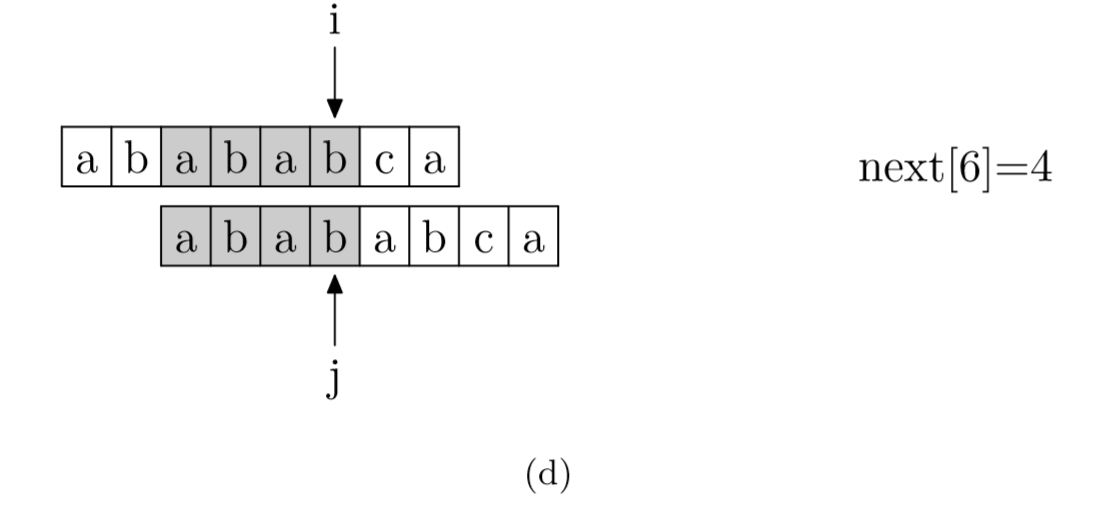
next_d
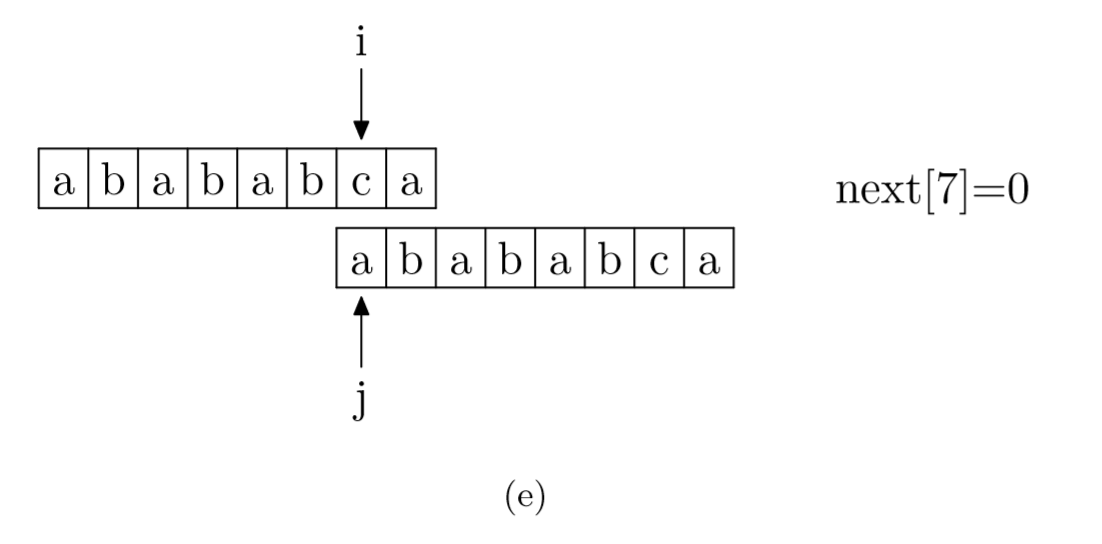
next_e

题解

题解一：暴力

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public int StrStr(string haystack, string needle) {
    int n = haystack.Length, m = needle.Length;
    for(int i = 0; i <= n - m; i++) {
        bool flag = true;
        for(int j = 0; j < m; j++) {
            if(haystack[i + j] != needle[j]) {
                flag = false;
                break;
            }
        }
        if(flag) {
            return i;
        }
    }
    return -1;
}

题解二：KMP

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
public int StrStr(string haystack, string needle) {
    if(needle.Length == 0) return 0;
    int m = haystack.Length, n = needle.Length;
    int[] next = BuildNext(needle);
    //匹配haystack和needle
    for(int i = 0, j = 0; i < m; i++) {
        while(haystack[i] != needle[j] && j > 0) {
            j = next[j - 1];
        }
        if(haystack[i] == needle[j]) {
            j++;
        }
        if(j == n) {
            return i - n + 1;
        }
    }
    return -1;
}

int[] BuildNext(string needle) {
    int n = needle.Length;
    int[] next = new int[n];
    next[0] = 0; //初始值
    for(int i = 1, j = 0; i < n; i++) {
        //一直往前找直到j = 0
        while(needle[j] != needle[i] && j > 0) {
            j = next[j - 1];
        }
        if(needle[i] == needle[j]) {
            j++;
        }
        next[i] = j;
    }
    return next;
}